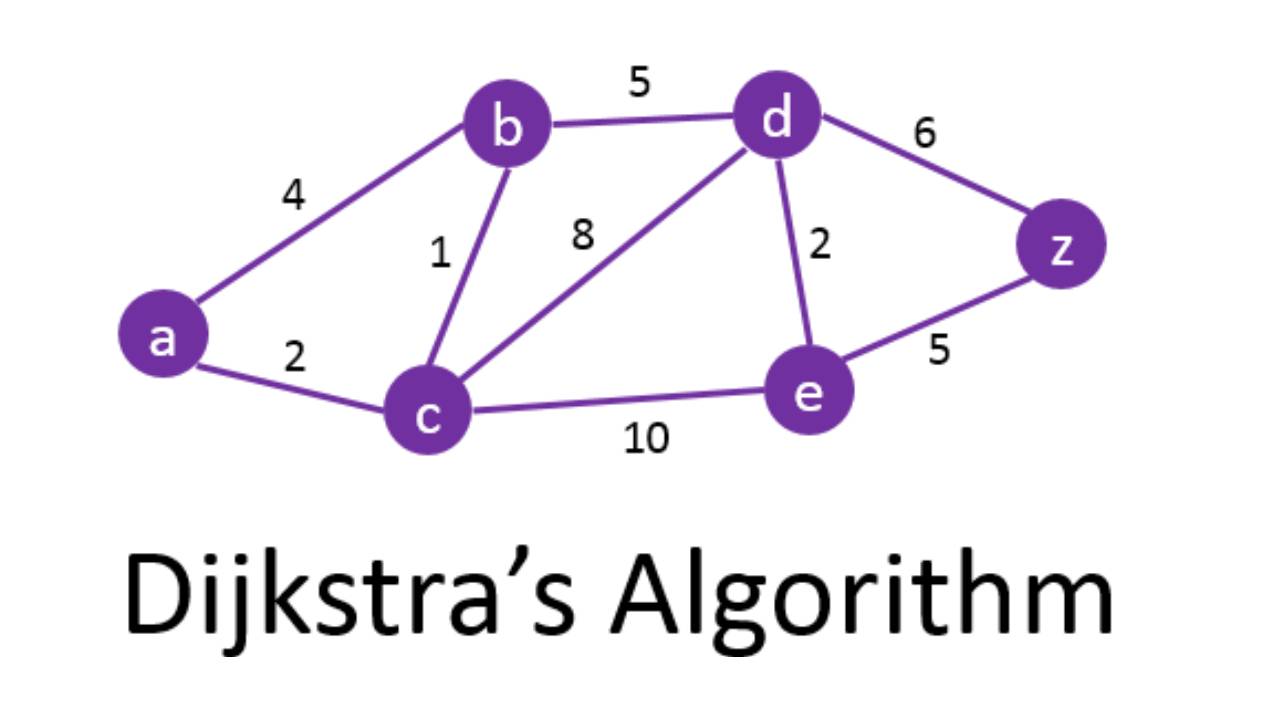
Dijkstra算法
Dijkstra 算法是一种快速,便利地计算非负权图上单源最短路的算法。什么?你问我什么是图?好吧,让我们从头开始。图说白了就是许多连线的点,可以近似为城市和中间的路。图分为有向图和无向图,可以近似为单向路和双向路。权值就是通过这条路所需的代价,是一个数字。而单源最短路就是两个点之间的最短路径。
而Dijkstra 算法的方法就是先将起点与其他点的举例设为inf,与自己的距离设为0. 再把点分为两种,已确定最短路长度的点集S,和未确定最短路长度的点集T. 一开始所有的点都属于T.
然后重复这些操作:
-
从T中,选取一个最短路长度最小的结点,移到S中.
-
对那些刚刚被加入S集合的结点的所有出边执行松弛操作.
直到T为空,算法结束.
至于什么是出边,就是可以出去的单行道,什么是松弛,就类似dp,重新计算距离.
通常使用朴素做法或优先队列做法.
很简单对吧,那么你可以开始做题了。
P4779 【模板】单源最短路径(标准版)
题目描述
给定一个n个点,m条有向边的带非负权图,请你计算从s出发,到每个点的距离.
数据保证你能从s出发到任意点.输入格式
第一行为三个正整数n,m,s. 第二行起m行,每行三个非负整数u[i],v[i],w[i],表示从 u[i]到v[i]有一条权值为w[i]的有向边.
输出格式
输出一行n个空格分隔的非负整数,表示s到每个点的距离。`
既然是模板题,那就直接上模板吧!
1 | |
你看懂了吗?很好!那么我们再来做一道题练练手!
P1629 邮递员送信
题目描述
有一个邮递员要送东西,邮局在节点1. 他总共要送n−1样东西,其目的地分别是节点2到节点n. 由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有m条道路. 这个邮递员每次只能带一样东西,并且运送每件物品过后必须返回邮局. 求送完这n−1样东西并且最终回到邮局最少需要的时间.
输入格式
第一行包括两个整数,n和m,表示城市的节点数量和道路数量.
第二行到第(m+1)行,每行三个整数,u,v,w,表示从u到v有一条通过时间为w的道路.输出格式
输出仅一行,包含一个整数,为最少需要的时间.
不难发现邮递员每次去要走最短路,回也要走最短路,那么只需要简单的正反跑Dijkstra就好了
1 | |

